Πολύ σωστό. Έχω πιάσει όπλα 3,6Kg (σκοπευτικά) και μου φάνηκαν αν όχι ελαφριά τουλάχιστον όχι βαριά και είχα πλάγιο 3150gr που κρέμαγε μπροστά, λες και είχες τσιμεντώσει τις κάννες.Μην μπερδεύουμε το ελαφρύ με το ζυγισμένο παιδιά.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Σκέφτομαι να αγοράσω.. ARXEIO
- Thread starter BeReT aKa RoBo aKa 1%
- Ημερομηνία δημιουργίας
- Status
- Not open for further replies.
Πως βρίσκουμε αν ένα όπλο είναι ζυγισμένο ;;;
Γεμίζουμε με φυσίγγια, επωμίζουμε κανονικά, βρίσκουμε τις θέσεις των χεριών στην λαβή και την πάπια, βρίσκουμε το μέσον της απόστασης αυτής, βρίσκουμε πόσο απέχει το σημείο αυτό από το κέντρο βάρους του όπλου.
Πόσο απέχει στην 304 ;;;
0 cm ;;;
Δεν υπάρχει ζυγισμένο όπλο.
Υπάρχουν μόνο αζύγιστα σε δεδομένο χρήστη, άλλα είναι πολύ και άλλα λίγο.
ΤΟ ΖΥΓΙΣΜΑ ΕΙΝΑΙ ΜΕΤΡΗΣΙΜΟ
12/5/15Μια εξαιρετική προσέγγιση από τον Γιάννη Μυριτζή μας δίνει χρησιμότατα τεχνικά εφόδια:
Καμιά λέξη όσο το «ζύγισμα» δεν εμφανίζεται τόσο συχνά κατά τις περιγραφές όπλων και καμιά έννοια στην οπλοτεχνική δεν είναι τόσο ασαφής όσο το «ζύγισμα του όπλου». Για πολλούς αναγνώστες είναι παραπλανητικό ένα σχόλιο σε περιοδικό ότι το τάδε μοντέλο είναι καλοζυγισμένο, ενώ πρόκειται απλώς για ένα υπερελαφρύ όπλο με μπάσκουλα από εργκάλ. Όμως το ζύγισμα δεν είναι προσωπική υπόθεση. Είναι μετρήσιμη ιδιότητα του όπλου, όπως μας έμαθε ο Gough Thomas, ο μόνος που επιχείρησε μια ποσοτική προσέγγιση στο ζήτημα. Σύμφωνα λοιπόν με αυτόν, το ζύγισμα περιγράφεται από δύο μεγέθη:
(1) Τη ροπή αδράνειας του όπλου και (2) την απόσταση του σημείου ισορροπίας του όπλου από την πρώτη σκανδάλη.
Τι είναι όμως η ροπή αδράνειας ενός σώματος; Ο ορισμός βρίσκεται σε σχολικά βιβλία φυσικής Λυκείου, που γράφτηκαν πριν ξεχαρβαλωθεί η μέση εκπαίδευση. Για να μη κουράσω τον αναγνώστη με φοβία στα μαθηματικά, θα προσπαθήσω αντί ορισμού να περιγράψω το μέγεθος. Η ροπή αδράνειας ενός σώματος ως προς ένα άξονα που περνά από το κέντρο βάρους του σώματος, εξαρτάται από τη μάζα του σώματος (βάρος λέμε στην καθομιλουμένη), αλλά και από την κατανομή της μάζας. Έτσι ένα σώμα που η μάζα του είναι κατανεμημένη μακριά από το κέντρου βάρους του έχει σχετικά μεγάλη ροπή αδράνειας. Ένα απλό παράδειγμα κάνει κατανοητή την έννοια. Ας θεωρήσουμε ένα δίσκο μάζας m και ακτίνας R, και ένα δακτύλιο με ίδια μάζα και ίδια ακτίνα. Αποδεικνύεται ότι η ροπή αδράνειας του δίσκου ως προς άξονα που περνά από το κέντρο βάρους και είναι κάθετος στο επίπεδό του, είναι και του δακτυλίου mR2, δηλαδή διπλάσια. Αυτό οφείλεται στο ότι η μάζα του δίσκου κατανέμεται σε αποστάσεις από μηδέν μέχρι R, ενώ ολόκληρη η μάζα του δακτυλίου είναι κατανεμημένη σε απόσταση R από το κέντρο βάρους. Ποιά είναι η φυσική σημασία της ροπής αδράνειας; Εκφράζει το μέτρο της αντίστασης του σώματος όταν επιχειρούμε να το θέσουμε σε περιστροφική κίνηση. Επομένως, ένας σφόνδυλος τίθεται σε περιστροφική κίνηση δυσκολότερα από ένα δίσκο ίδιας μάζας και ίδιας ακτίνας. Όμοια, δυσκολότερα θα φρενάρουμε ένα περιστρεφόμενο σφόνδυλο από ένα δίσκο. Την ιδιότητα αυτή εκμεταλλευόμαστε στο σφόνδυλο, που λόγω μεγάλης ροπής αδράνειας αποθηκεύει μεγάλη κινητική ενέργεια περιστροφής.
Ένα δεύτερο παράδειγμα θα μας οδηγήσει ευκολότερα στην κατανόηση της ροπής αδράνειας του τουφεκιού. Ας φανταστούμε ότι το τουφέκι έχει μήκος L και η μάζα του είναι ισοκατανεμημένη, προσομοιάζεται δηλαδή από ραβδί. Αποδεικνύεται ότι η ροπή αδράνειας του ραβδιού ως προς κάθετο άξονα που περνά από το κέντρο βάρους του, είναι .
Αν τώρα φανταστούμε ότι το τουφέκι έχει μήκος L και η μάζα του είναι συγκεντρωμένη εξ’ ίσου στα άκρα του, (προσομοιάζεται δηλαδή από αβαρές ραβδί με δύο μάζες m/2 στα άκρα του), προκύπτει ότι η ροπή αδράνειας του είναι δηλαδή εξαπλάσια του πρώτου. Η ροπή αδράνειας του υποθετικού μας τουφεκιού θα ήταν ακόμα μικρότερη του , αν η μάζα του ήταν συγκεντρωμένη κοντά στο κέντρο βάρος του.
Τα παραπάνω παραδείγματα δείχνουν ότι είναι δυνατός ο υπολογισμός της ροπής αδράνειας σωμάτων με γεωμετρικό σχήμα. Αυτό δεν είναι εφικτό για άμορφα σώματα όπως ένας μετεωρίτης, ή όχι γεωμετρικά καθορισμένο σχήμα, όπως μια καφετιέρα. Για την εύρεση της ροπής αδράνειας του όπλου ο Gough Thomas προτείνει το εξής πείραμα. Από ένα κατακόρυφο σύρμα κρέμεται μία ελαφρά οριζόντια σανίδα πάνω στην οποία τοποθετείται το όπλο.
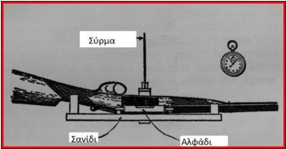
Το σύστημα τίθεται σε στροφική ταλάντωση περί τον κατακόρυφο άξονα και μετρούμε την περίοδο, T. Περίοδος είναι ο χρόνος στον οποίο γίνεται μία πλήρης ταλάντωση. Η μέτρηση είναι ακριβέστερη αν μετρήσουμε το χρόνο π.χ. δέκα ταλαντώσεων και διαιρέσουμε δια 10. Στα προαναφερθέντα σχολικά βιβλία φυσικής, π.χ. πρό του 1980, αποδεικνύεται ο τύπος που συνδέει την ροπή αδράνειας I, με την περίοδο της ταλάντωσης:

Το μέγεθος D εδώ, εκφράζει το μέτρο της στροφικής ακαμψίας του σύρματος, δηλαδή όσο περισσότερη ροπή απαιτεί ένα σύρμα για να το στρίψουμε κατά ορισμένη γωνία, τόσο μεγαλύτερο είναι το D. Αν γνωρίζαμε το D, τότε από τον παραπάνω τύπο θα υπολογίζαμε τη ροπή αδράνειας I, του όπλου μας. Αλλά η μέτρηση του D είναι δύσκολη οπότε καταφεύγουμε στο εξής τέχνασμα. Ας θεωρήσουμε και ένα άλλο όπλο που θα το θεωρούμε ως πρότυπο. Το πρότυπο μας έχει κάποια ροπή αδράνειας, Ι0, που φυσικά δεν την ξέρουμε. Αν το πρότυπο όπλο τεθεί σε στροφική ταλάντωση όπως πιο πάνω, θα έχει κάποια άλλη περίοδο T0, που θα δίνεται από τον τύπο,.

Το μέγεθος D, δεν αλλάζει, διότι είναι αποκλειστικό χαρακτηριστικό του σύρματος, δεν εξαρτάται δηλαδή από το αντικείμενο που κρεμούμε. Αν υψώσουμε στο τετράγωνο και στη συνέχεια διαιρέσουμε κατά μέλη τις παραπάνω εξισώσεις, προκύπτει,
Μαθηματικός Τύπος 3 (στο επόμενο)
Έτσι, βρίσκουμε τη ροπή αδράνειας I, του όπλου μας ως ποσοστό της πρότυπης I 0,
Μαθηματικός Τύπος 4 (στο επόμενο)
Αν για παράδειγμα έχουμε μετρήσει περιόδους, T = 0.5 sec και T0 = 0.6 sec (τα νούμερα είναι αυθαίρετα), τότε θα έχουμε ότι I = 0.695I0, δηλαδή η ροπή αδράνειας I, του όπλου μας είναι περίπου το 70% της πρότυπης I0. Η τελευταία εξίσωση μας επιτρέπει να εκφράσουμε την ροπή αδράνεια οποιουδήποτε όπλου ως ποσοστό της ροπής αδράνειας ενός πρότυπου όπλου. Για παράδειγμα, ο πίνακας των πλαγιόκαννων που παραθέτει ο Gough Thomas, δείχνει τις ροπές αδράνειας τριών δίκαννων, ως ποσοστά της ροπής αδράνειας ενός όπλου του Manton κατασκευής 1830 και βάρους 2.830.
Επειδή η ροπή αδράνειας εξαρτάται από τη μάζα (ή από το βάρος του όπλου), η μέθοδος έχει ένα μειονέκτημα που δεν αναφέρεται από τον Gough Thomas: μπορεί να εφαρμοσθεί μόνο για όπλα του ίδιου ή παραπλήσιου βάρους.
Μία δεύτερη παρατήρηση. Με την παραπάνω διαδικασία, μετρούμε τη ροπή αδράνειας ολόκληρου του συστήματος όπλο + σανίδα. Επειδή όμως μας ενδιαφέρει η συγκριτική σχέση μεταξύ όπλων, μπορούμε να αγνοήσουμε το παραπάνω σφάλμα. Αν η εγκατάσταση μας είναι βαριά ή θέλουμε οπωσδήποτε να λάβουμε υπ’ όψιν πόσο συμμετέχει η σανίδα στη συνολική ροπή αδράνειας, μπορούμε να εκλεπτύνουμε τους υπολογισμούς. Όποιος ενδιαφέρεται για τις λεπτομέρειες, μπορεί να με αναζητήσει στο διαδίκτυο και να μου στείλει ηλεκτρονικό μήνυμα.
Επαναλαμβάνουμε λοιπόν ότι κατά τον Gough Thomas, το ζύγισμα περιγράφεται από δυο μεγέθη:
(1) Τη ροπή αδράνειας του όπλου και (2) την απόσταση του σημείου ισορροπίας του όπλου από την πρώτη σκανδάλη.
(1) Μικρή ροπή αδράνειας σημαίνει ότι το μεγαλύτερο βάρος βρίσκεται ανάμεσα στα χέρια. Όπως προαναφέρθηκε, όπλο με μικρή ροπή αδράνειας εύκολα περιστρέφεται γύρω από το κέντρο βάρους του. Τότε το όπλο δείχνει ζωντανό. Θα το καταλάβουμε αν το πιάσουμε με τα δυο χέρια έτοιμοι προς επώμιση και το κουνήσουμε πάνω-κάτω περιστροφικά κατά το κατακόρυφο επίπεδο. Το όπλο με βάση από εργκάλ θα προδώσει αμέσως την κακή κατανομή βάρους, το βάρος δηλαδή βρίσκεται στα άκρα και όχι ανάμεσα στα χέρια.
(2) Το άλλο μέγεθος, που δείχνει το σημείο ισορροπίας του όπλου (το κέντρο βάρους με άλλα λόγια), δείχνει απλά αν το όπλο είναι οπισθόβαρο ή εμπροσθόβαρο. Εδώ, υπεισέρχεται πράγματι η υποκειμενική προτίμηση του κυνηγού. Οι Άγγλοι θεωρούν ως ιδανική απόσταση τα 10,5 εκατοστά. Μια καραμπίνα είναι πάντα εμπροσθόβαρη και ένα Darne είναι πάντα οπισθοβαρές. Ένα σουπερποζέ Chapuis Artisanal που έχω μετρήσει, ζυγιάζει στα 9.5 εκατοστά.
Χωρίς καμία ελιτίστικη διάθεση, πιστεύω ότι επειδή οι περισσότεροι κυνηγούν με καραμπίνες ή κακοζυγισμένα δίκαννα, αδυνατούν να αναγνωρίσουν ένα καλοζυγισμένο όπλο. Όποιος πάει περπατητό με ένα καλοζυγισμένο όπλο, πιστεύω πως δεν θα ξαναπιάσει καραμπίνα ή δίκαννο με αλουμινένια μπάσκουλα.
Ένα τελευταίο σχόλιο για όποιον αντέχει ακόμα το δασκαλίστικο ύφος μου. Λέγεται ότι ένα βαρύ αλλά καλοζυγισμένο όπλο, δείχνει πιο ζωντανό από ένα ελαφρύ και κακοζυγισμένο. Για να πεισθείτε κάνετε το εξής πείραμα. Λιώστε μολύβι, π.χ. σκάγια, και χύστε το σε κυλινδρικό καλούπι διαμέτρου 18mm, έτσι που να χωράει σε κάλυκα. Γεμίστε δυο κάλυκες με δυο τέτοια κυλινδρικά κομμάτια μολυβιού και βάλτε λίγη κόλα. Έχετε τώρα δυο «φυσίγγια» βάρους 130g περίπου το καθένα. Γεμίστε με αυτά ένα όπλο με βάση από εργκάλ (ή το συνηθισμένο σας όπλο). Έχετε τώρα ένα όπλο κατά 250g βαρύτερο. Κουνήστε το πάνω-κάτω περιστροφικά. Θα εκπλαγείτε από την αίσθηση.
Γιάννης Μυριτζής
Πανεπιστήμιο Αιγαίου
Τμήμα Επιστημών της Θάλασσας
Είμαι της ίδιας λογικής σε ότι αφορά την κατανομή του βάρους στα όπλα, αλλά αυτό βολεύει εμένα και όσους ρίχνουν γρήγορες, ενστικτωδεις τουφεκιές, νομίζω οι σκοπευτές και όσοι κάνουν καρτερατα κυνήγια προτιμούν όπλα με εμπροσθοβαρες τάσεις και αυξημενη στροφορμη γιατί βοηθάνε όσους εφαρμόζουν τεχνικές ελεγχόμενης προσκοπευσης.
Αν και με τη φυσική έτσι προσδιορίζεται, πρακτικά βολεύτηκα περισσότερο με ελαφριά και ζυγισμένα όπλα. Καθαρά προσωπικό και μόνο.Είμαι της ίδιας λογικής σε ότι αφορά την κατανομή του βάρους στα όπλα, αλλά αυτό βολεύει εμένα και όσους ρίχνουν γρήγορες, ενστικτωδεις τουφεκιές, νομίζω οι σκοπευτές και όσοι κάνουν καρτερατα κυνήγια προτιμούν όπλα με εμπροσθοβαρες τάσεις και αυξημενη στροφορμη γιατί βοηθάνε όσους εφαρμόζουν τεχνικές ελεγχόμενης προσκοπευσης.
Λογική τιμή φαίνεται , αρκεί η καλή κατάσταση να μην αποδειχθεί ριμαδι.
gvp9000
Banned
Με πέθανες ρε φίλεΤΟ ΖΥΓΙΣΜΑ ΕΙΝΑΙ ΜΕΤΡΗΣΙΜΟ
12/5/15
Μια εξαιρετική προσέγγιση από τον Γιάννη Μυριτζή μας δίνει χρησιμότατα τεχνικά εφόδια:
Καμιά λέξη όσο το «ζύγισμα» δεν εμφανίζεται τόσο συχνά κατά τις περιγραφές όπλων και καμιά έννοια στην οπλοτεχνική δεν είναι τόσο ασαφής όσο το «ζύγισμα του όπλου». Για πολλούς αναγνώστες είναι παραπλανητικό ένα σχόλιο σε περιοδικό ότι το τάδε μοντέλο είναι καλοζυγισμένο, ενώ πρόκειται απλώς για ένα υπερελαφρύ όπλο με μπάσκουλα από εργκάλ. Όμως το ζύγισμα δεν είναι προσωπική υπόθεση. Είναι μετρήσιμη ιδιότητα του όπλου, όπως μας έμαθε ο Gough Thomas, ο μόνος που επιχείρησε μια ποσοτική προσέγγιση στο ζήτημα. Σύμφωνα λοιπόν με αυτόν, το ζύγισμα περιγράφεται από δύο μεγέθη:
(1) Τη ροπή αδράνειας του όπλου και (2) την απόσταση του σημείου ισορροπίας του όπλου από την πρώτη σκανδάλη.
Τι είναι όμως η ροπή αδράνειας ενός σώματος; Ο ορισμός βρίσκεται σε σχολικά βιβλία φυσικής Λυκείου, που γράφτηκαν πριν ξεχαρβαλωθεί η μέση εκπαίδευση. Για να μη κουράσω τον αναγνώστη με φοβία στα μαθηματικά, θα προσπαθήσω αντί ορισμού να περιγράψω το μέγεθος. Η ροπή αδράνειας ενός σώματος ως προς ένα άξονα που περνά από το κέντρο βάρους του σώματος, εξαρτάται από τη μάζα του σώματος (βάρος λέμε στην καθομιλουμένη), αλλά και από την κατανομή της μάζας. Έτσι ένα σώμα που η μάζα του είναι κατανεμημένη μακριά από το κέντρου βάρους του έχει σχετικά μεγάλη ροπή αδράνειας. Ένα απλό παράδειγμα κάνει κατανοητή την έννοια. Ας θεωρήσουμε ένα δίσκο μάζας m και ακτίνας R, και ένα δακτύλιο με ίδια μάζα και ίδια ακτίνα. Αποδεικνύεται ότι η ροπή αδράνειας του δίσκου ως προς άξονα που περνά από το κέντρο βάρους και είναι κάθετος στο επίπεδό του, είναι και του δακτυλίου mR2, δηλαδή διπλάσια. Αυτό οφείλεται στο ότι η μάζα του δίσκου κατανέμεται σε αποστάσεις από μηδέν μέχρι R, ενώ ολόκληρη η μάζα του δακτυλίου είναι κατανεμημένη σε απόσταση R από το κέντρο βάρους. Ποιά είναι η φυσική σημασία της ροπής αδράνειας; Εκφράζει το μέτρο της αντίστασης του σώματος όταν επιχειρούμε να το θέσουμε σε περιστροφική κίνηση. Επομένως, ένας σφόνδυλος τίθεται σε περιστροφική κίνηση δυσκολότερα από ένα δίσκο ίδιας μάζας και ίδιας ακτίνας. Όμοια, δυσκολότερα θα φρενάρουμε ένα περιστρεφόμενο σφόνδυλο από ένα δίσκο. Την ιδιότητα αυτή εκμεταλλευόμαστε στο σφόνδυλο, που λόγω μεγάλης ροπής αδράνειας αποθηκεύει μεγάλη κινητική ενέργεια περιστροφής.
Ένα δεύτερο παράδειγμα θα μας οδηγήσει ευκολότερα στην κατανόηση της ροπής αδράνειας του τουφεκιού. Ας φανταστούμε ότι το τουφέκι έχει μήκος L και η μάζα του είναι ισοκατανεμημένη, προσομοιάζεται δηλαδή από ραβδί. Αποδεικνύεται ότι η ροπή αδράνειας του ραβδιού ως προς κάθετο άξονα που περνά από το κέντρο βάρους του, είναι .
Αν τώρα φανταστούμε ότι το τουφέκι έχει μήκος L και η μάζα του είναι συγκεντρωμένη εξ’ ίσου στα άκρα του, (προσομοιάζεται δηλαδή από αβαρές ραβδί με δύο μάζες m/2 στα άκρα του), προκύπτει ότι η ροπή αδράνειας του είναι δηλαδή εξαπλάσια του πρώτου. Η ροπή αδράνειας του υποθετικού μας τουφεκιού θα ήταν ακόμα μικρότερη του , αν η μάζα του ήταν συγκεντρωμένη κοντά στο κέντρο βάρος του.
Τα παραπάνω παραδείγματα δείχνουν ότι είναι δυνατός ο υπολογισμός της ροπής αδράνειας σωμάτων με γεωμετρικό σχήμα. Αυτό δεν είναι εφικτό για άμορφα σώματα όπως ένας μετεωρίτης, ή όχι γεωμετρικά καθορισμένο σχήμα, όπως μια καφετιέρα. Για την εύρεση της ροπής αδράνειας του όπλου ο Gough Thomas προτείνει το εξής πείραμα. Από ένα κατακόρυφο σύρμα κρέμεται μία ελαφρά οριζόντια σανίδα πάνω στην οποία τοποθετείται το όπλο.
View attachment 45096
Το σύστημα τίθεται σε στροφική ταλάντωση περί τον κατακόρυφο άξονα και μετρούμε την περίοδο, T. Περίοδος είναι ο χρόνος στον οποίο γίνεται μία πλήρης ταλάντωση. Η μέτρηση είναι ακριβέστερη αν μετρήσουμε το χρόνο π.χ. δέκα ταλαντώσεων και διαιρέσουμε δια 10. Στα προαναφερθέντα σχολικά βιβλία φυσικής, π.χ. πρό του 1980, αποδεικνύεται ο τύπος που συνδέει την ροπή αδράνειας I, με την περίοδο της ταλάντωσης:
View attachment 45097
Το μέγεθος D εδώ, εκφράζει το μέτρο της στροφικής ακαμψίας του σύρματος, δηλαδή όσο περισσότερη ροπή απαιτεί ένα σύρμα για να το στρίψουμε κατά ορισμένη γωνία, τόσο μεγαλύτερο είναι το D. Αν γνωρίζαμε το D, τότε από τον παραπάνω τύπο θα υπολογίζαμε τη ροπή αδράνειας I, του όπλου μας. Αλλά η μέτρηση του D είναι δύσκολη οπότε καταφεύγουμε στο εξής τέχνασμα. Ας θεωρήσουμε και ένα άλλο όπλο που θα το θεωρούμε ως πρότυπο. Το πρότυπο μας έχει κάποια ροπή αδράνειας, Ι0, που φυσικά δεν την ξέρουμε. Αν το πρότυπο όπλο τεθεί σε στροφική ταλάντωση όπως πιο πάνω, θα έχει κάποια άλλη περίοδο T0, που θα δίνεται από τον τύπο,.
View attachment 45098
Το μέγεθος D, δεν αλλάζει, διότι είναι αποκλειστικό χαρακτηριστικό του σύρματος, δεν εξαρτάται δηλαδή από το αντικείμενο που κρεμούμε. Αν υψώσουμε στο τετράγωνο και στη συνέχεια διαιρέσουμε κατά μέλη τις παραπάνω εξισώσεις, προκύπτει,
Μαθηματικός Τύπος 3 (στο επόμενο)
Έτσι, βρίσκουμε τη ροπή αδράνειας I, του όπλου μας ως ποσοστό της πρότυπης I 0,
Μαθηματικός Τύπος 4 (στο επόμενο)
Αν για παράδειγμα έχουμε μετρήσει περιόδους, T = 0.5 sec και T0 = 0.6 sec (τα νούμερα είναι αυθαίρετα), τότε θα έχουμε ότι I = 0.695I0, δηλαδή η ροπή αδράνειας I, του όπλου μας είναι περίπου το 70% της πρότυπης I0. Η τελευταία εξίσωση μας επιτρέπει να εκφράσουμε την ροπή αδράνεια οποιουδήποτε όπλου ως ποσοστό της ροπής αδράνειας ενός πρότυπου όπλου. Για παράδειγμα, ο πίνακας των πλαγιόκαννων που παραθέτει ο Gough Thomas, δείχνει τις ροπές αδράνειας τριών δίκαννων, ως ποσοστά της ροπής αδράνειας ενός όπλου του Manton κατασκευής 1830 και βάρους 2.830.
Επειδή η ροπή αδράνειας εξαρτάται από τη μάζα (ή από το βάρος του όπλου), η μέθοδος έχει ένα μειονέκτημα που δεν αναφέρεται από τον Gough Thomas: μπορεί να εφαρμοσθεί μόνο για όπλα του ίδιου ή παραπλήσιου βάρους.
Μία δεύτερη παρατήρηση. Με την παραπάνω διαδικασία, μετρούμε τη ροπή αδράνειας ολόκληρου του συστήματος όπλο + σανίδα. Επειδή όμως μας ενδιαφέρει η συγκριτική σχέση μεταξύ όπλων, μπορούμε να αγνοήσουμε το παραπάνω σφάλμα. Αν η εγκατάσταση μας είναι βαριά ή θέλουμε οπωσδήποτε να λάβουμε υπ’ όψιν πόσο συμμετέχει η σανίδα στη συνολική ροπή αδράνειας, μπορούμε να εκλεπτύνουμε τους υπολογισμούς. Όποιος ενδιαφέρεται για τις λεπτομέρειες, μπορεί να με αναζητήσει στο διαδίκτυο και να μου στείλει ηλεκτρονικό μήνυμα.
Επαναλαμβάνουμε λοιπόν ότι κατά τον Gough Thomas, το ζύγισμα περιγράφεται από δυο μεγέθη:
(1) Τη ροπή αδράνειας του όπλου και (2) την απόσταση του σημείου ισορροπίας του όπλου από την πρώτη σκανδάλη.
(1) Μικρή ροπή αδράνειας σημαίνει ότι το μεγαλύτερο βάρος βρίσκεται ανάμεσα στα χέρια. Όπως προαναφέρθηκε, όπλο με μικρή ροπή αδράνειας εύκολα περιστρέφεται γύρω από το κέντρο βάρους του. Τότε το όπλο δείχνει ζωντανό. Θα το καταλάβουμε αν το πιάσουμε με τα δυο χέρια έτοιμοι προς επώμιση και το κουνήσουμε πάνω-κάτω περιστροφικά κατά το κατακόρυφο επίπεδο. Το όπλο με βάση από εργκάλ θα προδώσει αμέσως την κακή κατανομή βάρους, το βάρος δηλαδή βρίσκεται στα άκρα και όχι ανάμεσα στα χέρια.
(2) Το άλλο μέγεθος, που δείχνει το σημείο ισορροπίας του όπλου (το κέντρο βάρους με άλλα λόγια), δείχνει απλά αν το όπλο είναι οπισθόβαρο ή εμπροσθόβαρο. Εδώ, υπεισέρχεται πράγματι η υποκειμενική προτίμηση του κυνηγού. Οι Άγγλοι θεωρούν ως ιδανική απόσταση τα 10,5 εκατοστά. Μια καραμπίνα είναι πάντα εμπροσθόβαρη και ένα Darne είναι πάντα οπισθοβαρές. Ένα σουπερποζέ Chapuis Artisanal που έχω μετρήσει, ζυγιάζει στα 9.5 εκατοστά.
Χωρίς καμία ελιτίστικη διάθεση, πιστεύω ότι επειδή οι περισσότεροι κυνηγούν με καραμπίνες ή κακοζυγισμένα δίκαννα, αδυνατούν να αναγνωρίσουν ένα καλοζυγισμένο όπλο. Όποιος πάει περπατητό με ένα καλοζυγισμένο όπλο, πιστεύω πως δεν θα ξαναπιάσει καραμπίνα ή δίκαννο με αλουμινένια μπάσκουλα.
Ένα τελευταίο σχόλιο για όποιον αντέχει ακόμα το δασκαλίστικο ύφος μου. Λέγεται ότι ένα βαρύ αλλά καλοζυγισμένο όπλο, δείχνει πιο ζωντανό από ένα ελαφρύ και κακοζυγισμένο. Για να πεισθείτε κάνετε το εξής πείραμα. Λιώστε μολύβι, π.χ. σκάγια, και χύστε το σε κυλινδρικό καλούπι διαμέτρου 18mm, έτσι που να χωράει σε κάλυκα. Γεμίστε δυο κάλυκες με δυο τέτοια κυλινδρικά κομμάτια μολυβιού και βάλτε λίγη κόλα. Έχετε τώρα δυο «φυσίγγια» βάρους 130g περίπου το καθένα. Γεμίστε με αυτά ένα όπλο με βάση από εργκάλ (ή το συνηθισμένο σας όπλο). Έχετε τώρα ένα όπλο κατά 250g βαρύτερο. Κουνήστε το πάνω-κάτω περιστροφικά. Θα εκπλαγείτε από την αίσθηση.
Γιάννης Μυριτζής
Πανεπιστήμιο Αιγαίου
Τμήμα Επιστημών της Θάλασσας
Γ@μησέ το ... ας είναι αζύγιστο αν είναι να κάνω όλα αυτά αχαχα

Βασικά απ ότι έχω διαβάσει υπάρχουν 2 μετρήσιμα πράγματα.
Το ένα το έγραψα.
Το άλλο είναι αυτό που έγραψες εσύ.
Όσο πιο μαζεμένο είναι το βάρος του όπλου στο κέντρο τόσο πιο μανιτζέβελο γίνεται (κάνεις λιγότερη προσπάθεια για περιστροφή στο κατακόρυφο επίπεδο) ... Βοηθά και στην επώμιση.
Αλλά τα πάντα είναι συνήθεια και αίσθηση !!!
Και αυτές αλλάζουν ανάλογα το άτομο.
Αν ρίχνεις χρόνια με αζύγιστο, το ζυγισμένο θα σου φαίνεται αζύγιστο
gvp9000
Banned
Όπλο σκυλί, απλά δεν ξέρω αν είναι ζωντανό η ψόφιο.
...είναι πολύ καλός ο Μυριτζής Βασίλη...Με πέθανες ρε φίλε
Γ@μησέ το ... ας είναι αζύγιστο αν είναι να κάνω όλα αυτά αχαχα
Βασικά απ ότι έχω διαβάσει υπάρχουν 2 μετρήσιμα πράγματα.
Το ένα το έγραψα.
Το άλλο είναι αυτό που έγραψες εσύ.
Όσο πιο μαζεμένο είναι το βάρος του όπλου στο κέντρο τόσο πιο μανιτζέβελο γίνεται (κάνεις λιγότερη προσπάθεια για περιστροφή στο κατακόρυφο επίπεδο) ... Βοηθά και στην επώμιση.
Αλλά τα πάντα είναι συνήθεια και αίσθηση !!!
Και αυτές αλλάζουν ανάλογα το άτομο.
Αν ρίχνεις χρόνια με αζύγιστο, το ζυγισμένο θα σου φαίνεται αζύγιστο
Νομίζω εν κατακλείδι αν κάμουμε το πείραμα που λέει με τα φυσίγγια σ' ένα δίκαννο, ίσως πραγματικά εκπλαγούμε!
Για εμένα χωρίς να είμαι ειδικός σε οτιδήποτε έχει σχέση με τα όπλα, το όπλο σου είναι ζυγισμένο και δεν κουράζει. Γιατί άμα σου δώσω την Mossberg 590 τη δική μου και πας να τη βάλεις στο χέρι σου όπως στη φωτογραφία που ανέβασες, το όπλο θα πέσει με δύναμη από τη μεριά της κάννης. Φοβερά κουραστικό όπλο η 590 για κυνήγι που απαιτεί περπάτημα. Στο σκοπευτήριο αυτό βέβαια δεν είναι πρόβλημα και δε φαίνεται.Το ξέρω Ηλία αλλά η αίσθηση αλλάζει από άνθρωπο σε άνθρωπο. Αυτό θέλω να πω.
Εμένα πχ ούτε η μ2 ούτε η 1187 μου φαίνονται μπροστόβαρες.
Αυτό τι σημαίνει ; Ότι είναι ζυγισμένες ;;;
Ούτε φυσικά τις μέτρησα στο εκατοστό ποτέ.
Εδώ το όπλο έχει σίγουρα 2 winchester double x 3" στην αποθήκη ... Στην θαλάμη δεν έχει φυσίγγι ...
Είναι ζυγισμένο ή αζύγιστο ;;;
Ρωτάω ... δεν προσπαθώ να αποδείξω κάτι.
View attachment 45086
gvp9000
Banned
Μια χαρά τα λέει ... Και έχει δίκιο....είναι πολύ καλός ο Μυριτζής Βασίλη...
Νομίζω εν κατακλείδι αν κάμουμε το πείραμα που λέει με τα φυσίγγια σ' ένα δίκαννο, ίσως πραγματικά εκπλαγούμε!
Δεν χρειάζεται καν να κάνεις το πείραμα.
Θα υπάρχει διαφορετική αίσθηση ...
Αλλά με 250γρ παραπάνω στην βάση !!!
gvp9000
Banned
Γιατί ποιος είναι ειδικός ;;;Για εμένα χωρίς να είμαι ειδικός σε οτιδήποτε έχει σχέση με τα όπλα, το όπλο σου είναι ζυγισμένο και δεν κουράζει. Γιατί άμα σου δώσω την Mossberg 590 τη δική μου και πας να τη βάλεις στο χέρι σου όπως στη φωτογραφία που ανέβασες, το όπλο θα πέσει με δύναμη από τη μεριά της κάννης. Φοβερά κουραστικό όπλο η 590 για κυνήγι που απαιτεί περπάτημα. Στο σκοπευτήριο αυτό βέβαια δεν είναι πρόβλημα και δε φαίνεται.
Μόνο αυτός ... Δείτε τι λέει
https://www.hunterslife.gr/forums/threads/Σκοπευτικα-οπλα-μεσης-κατηγοριας.3386/page-8#post-551110
Διαβάστε πριν και μετά ...
Από φωτό πάντως....εντεχνως τραβηγμένη;Λογική τιμή φαίνεται , αρκεί η καλή κατάσταση να μην αποδειχθεί ριμαδι.
θελει προσοχη σε αυτα συνηθως τς εχουν σκισει της es 100 σε αυτα τα λεφτα αξιζει κατι αν ειναι σε νορμαλ κατασταση!!Λογική τιμή φαίνεται , αρκεί η καλή κατάσταση να μην αποδειχθεί ριμαδι.
Όπως και να έχει η αγορά μεταχειρισμένου θέλει έλεγχο από οπλουργο ,ακόμη και αν εκ πρώτης όψεως φαίνεται αστέρι.Από φωτό πάντως....εντεχνως τραβηγμένη;
Σήμερα μάλλον θα δω μια vitoria υποψήφια . Θα ενημερώσω σχετικάΌπως και να έχει η αγορά μεταχειρισμένου θέλει έλεγχο από οπλουργο ,ακόμη και αν εκ πρώτης όψεως φαίνεται αστέρι.
...με το καλό Κωστή!...άντε και στα στέφανα!...αν είναι καλό κορίτσι!!!Σήμερα μάλλον θα δω μια vitoria υποψήφια . Θα ενημερώσω σχετικά

- Status
- Not open for further replies.
Share:





