Και πολλα τα λες τα 40 αρια τοτε θα ειχαν και 350 μ/δ !!!Παλιότερα έριχνα κ εγώ πολύ χοντρά σκάγια.
Τελευταία βάζω νο7 πρώτο κ μετά 6αρι.
Αυτό με τα διαμπερή το είδα σε πέρδικες με χοντρά νίκελ σκάγια κ με γρήγορα φυσιγγια με απλά σκάγια κ sipe σε νορμαλ καιρό.
Οι semi magnum γομωσεις με χοντρά σκάγια του τότε καιρού ήταν πράγματι πολύ αποδοτικές. Χωρίς να έχω μετρήσει πιστεύω ότι ήταν γύρω στα 370-380μ/σ.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Βλητικές Δοκιμές - Αρχείο
- Thread starter BeReT aKa RoBo aKa 1%
- Ημερομηνία δημιουργίας
- Status
- Not open for further replies.
Θα ήταν χρήσιμο αν ο Βασίλης μας έγραφε πχ για πέρδικα σε 5 με 10 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380 και τι με 410 . Στην πράξη η διαφορά θα είναι μικρότερη λόγω μικρότερης παραμόρφωσης, όσο για προσκοπευσεις κλπ είναι νομίζω το ίδιο. Ίσως πρέπει να ξανά ανακαλύψουμε τις κυνηγετικες ταχύτητες, όσο πιο γρήγορες δεν σημαίνει απαραίτητα πιο αποδοτικές.
gvp9000
Banned
πέρδικα σε 10 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380Θα ήταν χρήσιμο αν ο Βασίλης μας έγραφε πχ για πέρδικα σε 5 με 10 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380 και τι με 410 . Στην πράξη η διαφορά θα είναι μικρότερη λόγω μικρότερης παραμόρφωσης, όσο για προσκοπευσεις κλπ είναι νομίζω το ίδιο. Ίσως πρέπει να ξανά ανακαλύψουμε τις κυνηγετικες ταχύτητες, όσο πιο γρήγορες δεν σημαίνει απαραίτητα πιο αποδοτικές.
Διάτρηση 62μ
Ενέργεια 52μ
πέρδικα σε 10 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 410
Διάτρηση 65μ
Ενέργεια 55μ
============================
πέρδικα σε 5 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380
Διάτρηση 61μ
Ενέργεια 51μ
πέρδικα σε 5 βαθμούς θερμοκρασία, το ν 6( 2,7), τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 410
Διάτρηση 63μ
Ενέργεια 54μ
Όπου "διάτρηση" η απόσταση που έχει μεμονωμένο σφαιρικό σκάγι την ικανότητα να τρυπήσει 0,75" jel 20%
Όπου "ενέργεια" η απόσταση που έχει μεμονωμένο σφαιρικό σκάγι ενέργεια 1 ftlb
Ευχαριστώ Βασίλη, όπως το υποπτευομουν, σχεδόν τα ίδια ,και να υποθέσω ότι και στην διαφορά απαιτούμενης προσκοπευσης, μια από τα ίδια. Τελικά αντί να βλέπουμε την ουσία, ψάχνουμε τρόπους να δυσκολεψουμε τους εαυτούς μας, σήμερα διάβασα σε ιταλικό φόρουμ, έναν ειδικό που μίλαγε για μια δοκιμή σε κανονάκι στα 36 γραμμάρια με Nobel Glasgow 62,εξαιρετική παλιά διβασικη πυρίτιδα. Οι περισσότεροι έγραφαν πως τους φαινόταν λίγο αναιμική, γιατί ενώ έβγαζε ταχύτητα 400+ μ/δ, με μικρό μάλιστα χρόνο κάνης, είχε χαμηλές σχετικά πιέσεις, 660bar. Δηλαδή που καταντήσαμε, να έχουμε συνηθίσει τα 750 και 850 bar για ένα φυσίγγι 36 γραμμάρια, και όταν προκύπτει κάτι καλύτερο αντί για αποδοχή να ψάχνουμε να το αντικαταστησουμε με αυτά που μας έχουν συνηθίσει και ας είναι υποδεέστερα.
Για βάλε για 9 αρακι που ρίχνω εγώ να δω αν ανταποκρίνεται η μελέτη στα μέτρα Βασίλη.
gvp9000
Banned
πέρδικα σε 10 βαθμούς θερμοκρασία, το ν 9, τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380Για βάλε για 9 αρακι που ρίχνω εγώ να δω αν ανταποκρίνεται η μελέτη στα μέτρα Βασίλη.
Διάτρηση 38μ
Ενέργεια 21μ
πέρδικα σε 10 βαθμούς θερμοκρασία, το ν 9, τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 410
Διάτρηση 40μ
Ενέργεια 23μ
============================
πέρδικα σε 5 βαθμούς θερμοκρασία, το ν 9, τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 380
Διάτρηση 37μ
Ενέργεια 21μ
πέρδικα σε 5 βαθμούς θερμοκρασία, το ν 9, τι μέγιστο ωφέλιμο βεληνεκές έχει με αρχική 410
Διάτρηση 39μ
Ενέργεια 23μ
Όπου "διάτρηση" η απόσταση που έχει μεμονωμένο σφαιρικό σκάγι την ικανότητα να τρυπήσει 0,75" (19mm) jel 20%
Όπου "ενέργεια" η απόσταση που έχει μεμονωμένο σφαιρικό σκάγι ενέργεια 1 ftlb
Νομίζω πως για την επάρκεια ή όχι ενός σκαγιου, αρκεί η διάτρηση ,η ενέργεια είναι λίγο αποπροσανατολιστικη, μπορεί δηλαδή ένα σκαγι λόγω μεγάλης διαμέτρου, άρα βάρους να έχει στα χαρτιά την απαιτούμενη ενέργεια, και να μην έχει την απαιτούμενη διάτρηση.
Μπορεί οι λειοκανες να μην είναι πιο χοντρές. Ή μπορεί να είναι ελάχιστα πιο χοντρές, και να μην παίζει ρόλο και να μην υπάρχει πρόβλημα με την πάπια.Η Benelli λέει ότι οι ραβδωτές 12άρες κάνες (slug) χρειάζονται διαφορετική πάπια για την τοποθέτησή τους στο όπλο. Άρα, είναι πιο "χοντρές" εξωτερικά.
Δεν λέει το ίδιο για τις λειόκανες κάνες slug.
gvp9000
Banned
Θα σας πω μερικά λόγια για το προγραμματάκι που χρησιμοποιώ και το οποίο μπορείτε να βρείτε και εσείς στο "φυσίγγια για αγριόχηνες".
1. Εγώ απλά μετέφερα σε excel την βασική δουλειά και τις εξισώσεις που έχουν παραχθεί από έναν αμερικάνο μαθηματικό (E. J. Allen) και μάλιστα τα αποτελέσματα έχουν διασταυρωθεί πειραματικά. Οι διασταυρώσεις που έχει κάνει φαίνονται στην εργασία του.
https://www.sciencedirect.com/science/article/pii/S2214914717301459
2. Τα ΒΑΣΙΚΑ ΜΕΓΕΘΗ που εξάγει το πρόγραμμα δηλαδή η ταχύτητα σε διάφορες αποστάσεις, οι χρόνοι, η πτώση των σκαγιών λόγω βαρύτητας, η εκτροπή λόγω πλαγίου ανέμου έχουν διασταυρωθεί επίσης (από εμένα) με τα αποτελέσματα που βγάζει το πρόγραμμα του συγχωρεμένου Ed Lowry (βλητικού της Winchester) ...
αυτά τα βασικά μεγέθη τα θεωρώ πάρα πολύ ακριβή !!!
από αυτά τώρα τα βασικά μεγέθη, παράγονται η ενέργεια σε διάφορες αποστάσεις και η προσκόπευση.
Και αυτά τα θεωρώ πολύ ακριβή γιατί ουσιαστικά τα επιπλέον μεγέθη που μπαίνουν μέσα στον υπολογισμό τους είναι στάνταρ !!! και έχουν επαληθευτεί πάλι με το πρόγραμμα του Ed Lowry.
Σε όλα τα παραπάνω υπάρχει και δεύτερη επιβεβαίωση από άλλο πρόγραμμα το KPY Shotshell Ballistics.
Άρα ουσιαστικά τα αποτελέσματα σε όσα μεγέθη γράφω παραπάνω είναι σωστά.
Όταν λέω ΣΩΣΤΑ εννοώ ότι 3 ανεξάρτητοι άνθρωποι έχουν δουλέψει στο ίδιο πρόβλημα και παράγουν σχεδόν τα ίδια αποτελέσματα.
Άρα (εγώ τουλάχιστον) τα εμπιστεύομαι απόλυτα.
Μην ξεχνάτε όμως ένα πολύ βασικό πράγμα.
Αυτά είναι μαθηματικά !!!
Αν το πρόγραμμα βγάλει μια ταχύτητα πχ 200m/s σε μια απόσταση προφανώς δεν θα έχουν όλα τα σκάγια αυτή την ταχύτητα γιατί κάποια θα είναι παραμορφωμένα ... το πρόγραμμα προυποθέτει σφαιρικά σκάγια.
Κάποιος θα έλεγε ότι αφού προυποθέτει σφαιρικά σκάγια, που ουσιαστικά δεν υπάρχουν, το πρόγραμμα είναι άχρηστο.
Αυτό δεν ισχύει γιατί έχουν γίνει πραγματικές δοκιμές και οι μετρήσεις επαληθεύονται πειραματικά.
3.
α) ελάχιστη απαιτούμενη ενέργεια καταβολής,
β) μέγιστη απόσταση καταβολής λόγω ενέργειας σκαγιών,
γ) ελάχιστη απαιτούμενη διάτρηση για καταβολή,
δ) μέγιστη απόσταση καταβολής λόγω διάτρησης ...
Σε αυτά τα 4 αποτελέσματα μπορεί να υπάρχουν αντιρρήσεις και είναι λογικό.
Καταρχήν είπαμε ότι οι ενέργειες υπολογίζονται "σωστά".
Οι διατρήσεις σε 20% βαλλιστικό τζελ πάλι υπολογίζονται "σωστά" (το σωστά σημαίνει ότι βγάζει τα ίδια αποτελέσματα με το πρόγραμμα του Ed Lowry επικεφαλή βλητικού της Winchester).
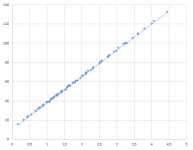
Δείτε εδώ την ταύτιση των αποτελεσμάτων.
Με την διακεκομμένη γραμή είναι οι διατρήσεις που βγάζει το πρόγραμμα και με τελείες αυτά που βγάζει το πρόγραμμα του Ed Lowry.
Σχεδόν απόλυτη ταύτιση.
Άρα και οι διατρήσεις σε 20% βαλλιστικό τζελ υπολογίζονται "σωστά".
ΤΟ ΜΕΓΑΛΟ ΠΡΟΒΛΗΜΑ ΕΙΝΑΙ
1. Η ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
2. Η ΕΛΑΧΙΣΤΗ ΔΙΑΤΡΗΣΗ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
Καταλαβαίνετε ότι αυτά τα μεγέθη δεν είναι στάνταρ, δεν υπάρχει σωστό και λάθος, δεν υπάρχει κάτι σίγουρο, τα νούμερα είναι ενδεικτικά, με λίγα λόγια μπορεί να υπάρχουν αντιρρήσεις.
Σε κάποια θηράματα έχω βρει πληροφορίες στο internet (κυρίως όσον αφορά την ενέργεια) αλλά σε κάποια θηράματα και για την διάτρηση.
Στα υπόλοιπα θηράματα ΕΒΑΛΑ ΕΓΩ ΤΙΜΕΣ ΕΝΤΕΛΩΣ ΑΥΘΑΙΡΕΤΑ με βάση αυτό που πιστεύω σωστό.
Το αυθαίρετα σημαίνει ότι δεν έχω επαληθεύσει τις τιμές με κάποια άλλη πηγή στο internet.
Πχ στην απαιτούμενη διάτρηση στον λαγό έβαλα αυθαίρετα τιμή 1,5 ίντσα σε βαλλιστικό τζελ 20%.
Υπάρχουν πολλές παραπομπές στο internet ότι η απαιτούμενη διάτρηση για πρασινοκέφαλο είναι 2 ίντσες σε βαλλιστικό τζελ 20%.
ΕΚΤΙΜΩ ΛΟΙΠΟΝ ΟΤΙ ΑΦΟΥ ΤΟ ΠΡΑΣΙΝΙ ΘΕΛΕΙ 2 ΙΝΤΣΕΣ Ο ΛΑΓΟΣ ΘΕΛΕΙ 1,5 ΙΝΤΣΑ.
Αυτό επηρρεάζει την μέγιστη απόσταση καταβολής, σαν αυτές που εδωσα παραπάνω.
Για να μην κάθομαι να ψειρίζω την μαϊμού έχω χωρίσει τα θηρεύσιμα σε 6 κατηγορίες.
Μικρά θηράματα
Μεσαία θηράματα
Πρασινοκέφαλη
Χήνα
Λαγός
Αγριογούρουνο
Η ελάχιστη ενέργεια καταβολής που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ft⋅lbf
Μεσαία θηράματα 1 ft⋅lbf
Πρασινοκέφαλη 2 ft⋅lbf
Χήνα 4 ft⋅lbf
Λαγός 1,5 ft⋅lbf
Αγριογούρουνο 90 ft⋅lbf
Η ελάχιστη διάτρηση καταβολής (σε 20% βαλλιστικό τζελ) που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ίντσες
Μεσαία θηράματα 0,75 ίντσες
Πρασινοκέφαλη 1,5 ίντσες
Χήνα 2,25 ίντσες
Λαγός 1 ίντσα
Αγριογούρουνο 7 ίντσες
Οποιαδήποτε πρόταση για αλλαγή η αναφορά στο internet είναι δεκτή.
Μην ξεχνάμε ένα πολύ βασικό πράγμα ...
Τα παραπάνω δεν λαμβάνουν υπόψη την κατανομή και αναφέρονται σε 1 μόνο σκάγι !!!
Όταν βλέπετε λοιπόν αποστάσεις πχ 60m αυτό δεν σημαίνει ότι αν τουφεκίσετε το θήραμα στα 60 θα πέσει.
Σημαίνει ότι αν ένα ΜΟΝΑΔΙΚΟ σκάγι τύχει και χτυπήσει το θήραμα στα 60m αυτό το σκάγι θα έχει την ελάχιστη απαιτούμενη ενέργεια (που για κάποια θηράματα έχει οριστεί αυθαίρετα από εμένα) ή την ελάχιστη απαιτούμενη διάτρηση (που για κάποια θηράματα έχει οριστεί πάλι αυθαίρετα από εμένα).
Για τον @ΝίκοςΠ
Νίκο η διάτρηση που δίνω είναι σε 20% βαλλιστικό τζελ όχι σε χαρτί ή εξώφυλλα που είναι πιο χοντρά.
Το 20% βαλλιστικό τζελ προσομοιάζει ζωικό ιστό.
Όταν λοιπόν γράφω 1 ίντσα σε 20% βαλλιστικό τζελ σημαίνει ότι αν πάρεις ένα κομμάτι ψαχνό κρέας και το βάλεις στα μέτρα αυτά θα βρεις σκάγια που κατα μέσο όρο θα έχουν τρυπήσει το κρέας κατά 1 ίντσα = 25 χιλιοστά περίπου.
Κάποια δεν θα έχουν τρυπήσει καθόλου !!!!
Άλλα μπορεί να έχουν τρυπήσει 1,5 ίντσα.
Ο μέσος όρος είναι η 1 ίντσα.
Ελπίζω να σας έδωσα να καταλάβετε κάποια πράγματα περισσότερο και να μην σας μπέρδεψα.
Μην θεωρείτε ευαγγέλιο τα νούμερα, δείτε τα σαν ενδεικτικές τιμές και χρήσιμα για συγκρίσεις ....
1. Εγώ απλά μετέφερα σε excel την βασική δουλειά και τις εξισώσεις που έχουν παραχθεί από έναν αμερικάνο μαθηματικό (E. J. Allen) και μάλιστα τα αποτελέσματα έχουν διασταυρωθεί πειραματικά. Οι διασταυρώσεις που έχει κάνει φαίνονται στην εργασία του.
https://www.sciencedirect.com/science/article/pii/S2214914717301459
2. Τα ΒΑΣΙΚΑ ΜΕΓΕΘΗ που εξάγει το πρόγραμμα δηλαδή η ταχύτητα σε διάφορες αποστάσεις, οι χρόνοι, η πτώση των σκαγιών λόγω βαρύτητας, η εκτροπή λόγω πλαγίου ανέμου έχουν διασταυρωθεί επίσης (από εμένα) με τα αποτελέσματα που βγάζει το πρόγραμμα του συγχωρεμένου Ed Lowry (βλητικού της Winchester) ...
αυτά τα βασικά μεγέθη τα θεωρώ πάρα πολύ ακριβή !!!
από αυτά τώρα τα βασικά μεγέθη, παράγονται η ενέργεια σε διάφορες αποστάσεις και η προσκόπευση.
Και αυτά τα θεωρώ πολύ ακριβή γιατί ουσιαστικά τα επιπλέον μεγέθη που μπαίνουν μέσα στον υπολογισμό τους είναι στάνταρ !!! και έχουν επαληθευτεί πάλι με το πρόγραμμα του Ed Lowry.
Σε όλα τα παραπάνω υπάρχει και δεύτερη επιβεβαίωση από άλλο πρόγραμμα το KPY Shotshell Ballistics.
Άρα ουσιαστικά τα αποτελέσματα σε όσα μεγέθη γράφω παραπάνω είναι σωστά.
Όταν λέω ΣΩΣΤΑ εννοώ ότι 3 ανεξάρτητοι άνθρωποι έχουν δουλέψει στο ίδιο πρόβλημα και παράγουν σχεδόν τα ίδια αποτελέσματα.
Άρα (εγώ τουλάχιστον) τα εμπιστεύομαι απόλυτα.
Μην ξεχνάτε όμως ένα πολύ βασικό πράγμα.
Αυτά είναι μαθηματικά !!!
Αν το πρόγραμμα βγάλει μια ταχύτητα πχ 200m/s σε μια απόσταση προφανώς δεν θα έχουν όλα τα σκάγια αυτή την ταχύτητα γιατί κάποια θα είναι παραμορφωμένα ... το πρόγραμμα προυποθέτει σφαιρικά σκάγια.
Κάποιος θα έλεγε ότι αφού προυποθέτει σφαιρικά σκάγια, που ουσιαστικά δεν υπάρχουν, το πρόγραμμα είναι άχρηστο.
Αυτό δεν ισχύει γιατί έχουν γίνει πραγματικές δοκιμές και οι μετρήσεις επαληθεύονται πειραματικά.
3.
α) ελάχιστη απαιτούμενη ενέργεια καταβολής,
β) μέγιστη απόσταση καταβολής λόγω ενέργειας σκαγιών,
γ) ελάχιστη απαιτούμενη διάτρηση για καταβολή,
δ) μέγιστη απόσταση καταβολής λόγω διάτρησης ...
Σε αυτά τα 4 αποτελέσματα μπορεί να υπάρχουν αντιρρήσεις και είναι λογικό.
Καταρχήν είπαμε ότι οι ενέργειες υπολογίζονται "σωστά".
Οι διατρήσεις σε 20% βαλλιστικό τζελ πάλι υπολογίζονται "σωστά" (το σωστά σημαίνει ότι βγάζει τα ίδια αποτελέσματα με το πρόγραμμα του Ed Lowry επικεφαλή βλητικού της Winchester).
Δείτε εδώ την ταύτιση των αποτελεσμάτων.
Με την διακεκομμένη γραμή είναι οι διατρήσεις που βγάζει το πρόγραμμα και με τελείες αυτά που βγάζει το πρόγραμμα του Ed Lowry.
Σχεδόν απόλυτη ταύτιση.
Άρα και οι διατρήσεις σε 20% βαλλιστικό τζελ υπολογίζονται "σωστά".

ΤΟ ΜΕΓΑΛΟ ΠΡΟΒΛΗΜΑ ΕΙΝΑΙ
1. Η ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
2. Η ΕΛΑΧΙΣΤΗ ΔΙΑΤΡΗΣΗ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
Καταλαβαίνετε ότι αυτά τα μεγέθη δεν είναι στάνταρ, δεν υπάρχει σωστό και λάθος, δεν υπάρχει κάτι σίγουρο, τα νούμερα είναι ενδεικτικά, με λίγα λόγια μπορεί να υπάρχουν αντιρρήσεις.
Σε κάποια θηράματα έχω βρει πληροφορίες στο internet (κυρίως όσον αφορά την ενέργεια) αλλά σε κάποια θηράματα και για την διάτρηση.
Στα υπόλοιπα θηράματα ΕΒΑΛΑ ΕΓΩ ΤΙΜΕΣ ΕΝΤΕΛΩΣ ΑΥΘΑΙΡΕΤΑ με βάση αυτό που πιστεύω σωστό.
Το αυθαίρετα σημαίνει ότι δεν έχω επαληθεύσει τις τιμές με κάποια άλλη πηγή στο internet.
Πχ στην απαιτούμενη διάτρηση στον λαγό έβαλα αυθαίρετα τιμή 1,5 ίντσα σε βαλλιστικό τζελ 20%.
Υπάρχουν πολλές παραπομπές στο internet ότι η απαιτούμενη διάτρηση για πρασινοκέφαλο είναι 2 ίντσες σε βαλλιστικό τζελ 20%.
ΕΚΤΙΜΩ ΛΟΙΠΟΝ ΟΤΙ ΑΦΟΥ ΤΟ ΠΡΑΣΙΝΙ ΘΕΛΕΙ 2 ΙΝΤΣΕΣ Ο ΛΑΓΟΣ ΘΕΛΕΙ 1,5 ΙΝΤΣΑ.
Αυτό επηρρεάζει την μέγιστη απόσταση καταβολής, σαν αυτές που εδωσα παραπάνω.
Για να μην κάθομαι να ψειρίζω την μαϊμού έχω χωρίσει τα θηρεύσιμα σε 6 κατηγορίες.
Μικρά θηράματα
Μεσαία θηράματα
Πρασινοκέφαλη
Χήνα
Λαγός
Αγριογούρουνο
Η ελάχιστη ενέργεια καταβολής που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ft⋅lbf
Μεσαία θηράματα 1 ft⋅lbf
Πρασινοκέφαλη 2 ft⋅lbf
Χήνα 4 ft⋅lbf
Λαγός 1,5 ft⋅lbf
Αγριογούρουνο 90 ft⋅lbf
Η ελάχιστη διάτρηση καταβολής (σε 20% βαλλιστικό τζελ) που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ίντσες
Μεσαία θηράματα 0,75 ίντσες
Πρασινοκέφαλη 1,5 ίντσες
Χήνα 2,25 ίντσες
Λαγός 1 ίντσα
Αγριογούρουνο 7 ίντσες
Οποιαδήποτε πρόταση για αλλαγή η αναφορά στο internet είναι δεκτή.
Μην ξεχνάμε ένα πολύ βασικό πράγμα ...
Τα παραπάνω δεν λαμβάνουν υπόψη την κατανομή και αναφέρονται σε 1 μόνο σκάγι !!!
Όταν βλέπετε λοιπόν αποστάσεις πχ 60m αυτό δεν σημαίνει ότι αν τουφεκίσετε το θήραμα στα 60 θα πέσει.
Σημαίνει ότι αν ένα ΜΟΝΑΔΙΚΟ σκάγι τύχει και χτυπήσει το θήραμα στα 60m αυτό το σκάγι θα έχει την ελάχιστη απαιτούμενη ενέργεια (που για κάποια θηράματα έχει οριστεί αυθαίρετα από εμένα) ή την ελάχιστη απαιτούμενη διάτρηση (που για κάποια θηράματα έχει οριστεί πάλι αυθαίρετα από εμένα).
Για τον @ΝίκοςΠ
Νίκο η διάτρηση που δίνω είναι σε 20% βαλλιστικό τζελ όχι σε χαρτί ή εξώφυλλα που είναι πιο χοντρά.
Το 20% βαλλιστικό τζελ προσομοιάζει ζωικό ιστό.
Όταν λοιπόν γράφω 1 ίντσα σε 20% βαλλιστικό τζελ σημαίνει ότι αν πάρεις ένα κομμάτι ψαχνό κρέας και το βάλεις στα μέτρα αυτά θα βρεις σκάγια που κατα μέσο όρο θα έχουν τρυπήσει το κρέας κατά 1 ίντσα = 25 χιλιοστά περίπου.
Κάποια δεν θα έχουν τρυπήσει καθόλου !!!!
Άλλα μπορεί να έχουν τρυπήσει 1,5 ίντσα.
Ο μέσος όρος είναι η 1 ίντσα.
Ελπίζω να σας έδωσα να καταλάβετε κάποια πράγματα περισσότερο και να μην σας μπέρδεψα.
Μην θεωρείτε ευαγγέλιο τα νούμερα, δείτε τα σαν ενδεικτικές τιμές και χρήσιμα για συγκρίσεις ....
Last edited:
gvp9000
Banned
Η διάτρηση είναι πολύ περίεργο πράγμα.
Η θεωρία λέει τα εξής.
Κανένας δεν μπορεί να υπολογίσει θεωρητικά (με μαθηματικά) την διάτρηση σε ένα σκάγι που παραμορφώνεται.
Άρα τα σκάγια θεωρούνται σχεδόν σφαιρικά (πρέπει να είναι σκληρά).
Όταν το σκάγι χτυπά πάνω σε μια επιφάνεια δεν ξεκινά αμέσως η διάτρηση ... το υλικό της επιφάνειας πιέζεται, άρα απορροφά ενέργεια από το σκάγι και μόλις το υλικό φτάσει στο όριο ρήξης τότε ξεκινά το ξετρύπημα.
Η διάτρηση είναι περίπου ανάλογη από την ταχύτητα που έχει παραμείνει στο σκάγι όταν ξεκίνησε η ρήξη !!!
Έτσι λοιπόν για να υπολογίσουμε την διάτρηση δεν φτάνει να ξέρουμε μόνο την ταχύτητα των σκαγιών όταν χτυπούν το θήραμα ΑΛΛΑ ΚΑΙ ΤΗΝ ΕΛΑΧΙΣΤΗ ΤΑΧΥΤΗΤΑ ΤΟΥ ΑΡΧΙΚΟΥ ΞΕΤΡΥΠΗΜΑΤΟΣ του υλικού.
Αυτή (η δεύτερη ταχύτητα) αφαιρείται από την πρώτη και όση ταχύτητα απομείνει δημιουργεί το μήκος της τρύπας στο υλικό.
Αν ένα σκάγι έχει μικρότερη ή ίση ταχύτητα με την ελάχιστη που μπορεί να δημιουργήσει ρήξη, προφανώς δεν θα τρυπήσει καθόλου !!!
Αν ένα σκάγι γίνει φακή ή δίσκος όταν χτυπήσει πάνω στο υλικό τότε η διάτρηση θα μειωθεί πάρα πολύ γιατί το εμβαδό αυξάνεται πολύ.
Αυτά για σήμερα με τις θεωρίες ... τώρα ας πειράξουμε κανέναν
Η θεωρία λέει τα εξής.
Κανένας δεν μπορεί να υπολογίσει θεωρητικά (με μαθηματικά) την διάτρηση σε ένα σκάγι που παραμορφώνεται.
Άρα τα σκάγια θεωρούνται σχεδόν σφαιρικά (πρέπει να είναι σκληρά).
Όταν το σκάγι χτυπά πάνω σε μια επιφάνεια δεν ξεκινά αμέσως η διάτρηση ... το υλικό της επιφάνειας πιέζεται, άρα απορροφά ενέργεια από το σκάγι και μόλις το υλικό φτάσει στο όριο ρήξης τότε ξεκινά το ξετρύπημα.
Η διάτρηση είναι περίπου ανάλογη από την ταχύτητα που έχει παραμείνει στο σκάγι όταν ξεκίνησε η ρήξη !!!
Έτσι λοιπόν για να υπολογίσουμε την διάτρηση δεν φτάνει να ξέρουμε μόνο την ταχύτητα των σκαγιών όταν χτυπούν το θήραμα ΑΛΛΑ ΚΑΙ ΤΗΝ ΕΛΑΧΙΣΤΗ ΤΑΧΥΤΗΤΑ ΤΟΥ ΑΡΧΙΚΟΥ ΞΕΤΡΥΠΗΜΑΤΟΣ του υλικού.
Αυτή (η δεύτερη ταχύτητα) αφαιρείται από την πρώτη και όση ταχύτητα απομείνει δημιουργεί το μήκος της τρύπας στο υλικό.
Αν ένα σκάγι έχει μικρότερη ή ίση ταχύτητα με την ελάχιστη που μπορεί να δημιουργήσει ρήξη, προφανώς δεν θα τρυπήσει καθόλου !!!
Αν ένα σκάγι γίνει φακή ή δίσκος όταν χτυπήσει πάνω στο υλικό τότε η διάτρηση θα μειωθεί πάρα πολύ γιατί το εμβαδό αυξάνεται πολύ.
Αυτά για σήμερα με τις θεωρίες ... τώρα ας πειράξουμε κανέναν
Το ήξερες επιδει εχεις μπενελλι ότι δεν τρυπάει ούτε χαρτοπετσέτατώρα ας πειράξουμε κανέναν

Βεβαίως υψηλότερες ταχύτητες από τις 370 & 380 μ/δλ στην κάννη (Vo) της S4!
Δεδομένου οτι οι ταχύτητες είναι V 10 στο Ελληνικό διαφημιστικό φυλλάδιο , έχουμε:
V10 330 μ/δλ = Vo 402 μ/δλ & V10 340 μ/δλ = Vo 418 μ/δλ (!)
Δες το φυλλάδιο των 70s για σκάγια Νο 7 (!)
Attachments
Θα σας πω μερικά λόγια για το προγραμματάκι που χρησιμοποιώ και το οποίο μπορείτε να βρείτε και εσείς στο "φυσίγγια για αγριόχηνες".
1. Εγώ απλά μετέφερα σε excel την βασική δουλειά και τις εξισώσεις που έχουν παραχθεί από έναν αμερικάνο μαθηματικό (E. J. Allen) και μάλιστα τα αποτελέσματα έχουν διασταυρωθεί πειραματικά. Οι διασταυρώσεις που έχει κάνει φαίνονται στην εργασία του.
https://www.sciencedirect.com/science/article/pii/S2214914717301459
2. Τα ΒΑΣΙΚΑ ΜΕΓΕΘΗ που εξάγει το πρόγραμμα δηλαδή η ταχύτητα σε διάφορες αποστάσεις, οι χρόνοι, η πτώση των σκαγιών λόγω βαρύτητας, η εκτροπή λόγω πλαγίου ανέμου έχουν διασταυρωθεί επίσης (από εμένα) με τα αποτελέσματα που βγάζει το πρόγραμμα του συγχωρεμένου Ed Lowry (βλητικού της Winchester) ...
αυτά τα βασικά μεγέθη τα θεωρώ πάρα πολύ ακριβή !!!
από αυτά τώρα τα βασικά μεγέθη, παράγονται η ενέργεια σε διάφορες αποστάσεις και η προσκόπευση.
Και αυτά τα θεωρώ πολύ ακριβή γιατί ουσιαστικά τα επιπλέον μεγέθη που μπαίνουν μέσα στον υπολογισμό τους είναι στάνταρ !!! και έχουν επαληθευτεί πάλι με το πρόγραμμα του Ed Lowry.
Σε όλα τα παραπάνω υπάρχει και δεύτερη επιβεβαίωση από άλλο πρόγραμμα το KPY Shotshell Ballistics.
Άρα ουσιαστικά τα αποτελέσματα σε όσα μεγέθη γράφω παραπάνω είναι σωστά.
Όταν λέω ΣΩΣΤΑ εννοώ ότι 3 ανεξάρτητοι άνθρωποι έχουν δουλέψει στο ίδιο πρόβλημα και παράγουν σχεδόν τα ίδια αποτελέσματα.
Άρα (εγώ τουλάχιστον) τα εμπιστεύομαι απόλυτα.
Μην ξεχνάτε όμως ένα πολύ βασικό πράγμα.
Αυτά είναι μαθηματικά !!!
Αν το πρόγραμμα βγάλει μια ταχύτητα πχ 200m/s σε μια απόσταση προφανώς δεν θα έχουν όλα τα σκάγια αυτή την ταχύτητα γιατί κάποια θα είναι παραμορφωμένα ... το πρόγραμμα προυποθέτει σφαιρικά σκάγια.
Κάποιος θα έλεγε ότι αφού προυποθέτει σφαιρικά σκάγια, που ουσιαστικά δεν υπάρχουν, το πρόγραμμα είναι άχρηστο.
Αυτό δεν ισχύει γιατί έχουν γίνει πραγματικές δοκιμές και οι μετρήσεις επαληθεύονται πειραματικά.
3.
α) ελάχιστη απαιτούμενη ενέργεια καταβολής,
β) μέγιστη απόσταση καταβολής λόγω ενέργειας σκαγιών,
γ) ελάχιστη απαιτούμενη διάτρηση για καταβολή,
δ) μέγιστη απόσταση καταβολής λόγω διάτρησης ...
Σε αυτά τα 4 αποτελέσματα μπορεί να υπάρχουν αντιρρήσεις και είναι λογικό.
Καταρχήν είπαμε ότι οι ενέργειες υπολογίζονται "σωστά".
Οι διατρήσεις σε 20% βαλλιστικό τζελ πάλι υπολογίζονται "σωστά" (το σωστά σημαίνει ότι βγάζει τα ίδια αποτελέσματα με το πρόγραμμα του Ed Lowry επικεφαλή βλητικού της Winchester).
Δείτε εδώ την ταύτιση των αποτελεσμάτων.
Με την διακεκομμένη γραμή είναι οι διατρήσεις που βγάζει το πρόγραμμα και με τελείες αυτά που βγάζει το πρόγραμμα του Ed Lowry.
Σχεδόν απόλυτη ταύτιση.
Άρα και οι διατρήσεις σε 20% βαλλιστικό τζελ υπολογίζονται "σωστά".
View attachment 45360
ΤΟ ΜΕΓΑΛΟ ΠΡΟΒΛΗΜΑ ΕΙΝΑΙ
1. Η ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
2. Η ΕΛΑΧΙΣΤΗ ΔΙΑΤΡΗΣΗ ΠΟΥ ΧΡΕΙΑΖΕΤΑΙ ΕΝΑ ΣΚΑΓΙ ΓΙΑ ΝΑ ΚΑΤΑΒΑΛΛΕΙ ΕΝΑ ΘΗΡΑΜΑ
Καταλαβαίνετε ότι αυτά τα μεγέθη δεν είναι στάνταρ, δεν υπάρχει σωστό και λάθος, δεν υπάρχει κάτι σίγουρο, τα νούμερα είναι ενδεικτικά, με λίγα λόγια μπορεί να υπάρχουν αντιρρήσεις.
Σε κάποια θηράματα έχω βρει πληροφορίες στο internet (κυρίως όσον αφορά την ενέργεια) αλλά σε κάποια θηράματα και για την διάτρηση.
Στα υπόλοιπα θηράματα ΕΒΑΛΑ ΕΓΩ ΤΙΜΕΣ ΕΝΤΕΛΩΣ ΑΥΘΑΙΡΕΤΑ με βάση αυτό που πιστεύω σωστό.
Το αυθαίρετα σημαίνει ότι δεν έχω επαληθεύσει τις τιμές με κάποια άλλη πηγή στο internet.
Πχ στην απαιτούμενη διάτρηση στον λαγό έβαλα αυθαίρετα τιμή 1,5 ίντσα σε βαλλιστικό τζελ 20%.
Υπάρχουν πολλές παραπομπές στο internet ότι η απαιτούμενη διάτρηση για πρασινοκέφαλο είναι 2 ίντσες σε βαλλιστικό τζελ 20%.
ΕΚΤΙΜΩ ΛΟΙΠΟΝ ΟΤΙ ΑΦΟΥ ΤΟ ΠΡΑΣΙΝΙ ΘΕΛΕΙ 2 ΙΝΤΣΕΣ Ο ΛΑΓΟΣ ΘΕΛΕΙ 1,5 ΙΝΤΣΑ.
Αυτό επηρρεάζει την μέγιστη απόσταση καταβολής, σαν αυτές που εδωσα παραπάνω.
Για να μην κάθομαι να ψειρίζω την μαϊμού έχω χωρίσει τα θηρεύσιμα σε 6 κατηγορίες.
Μικρά θηράματα
Μεσαία θηράματα
Πρασινοκέφαλη
Χήνα
Λαγός
Αγριογούρουνο
Η ελάχιστη ενέργεια καταβολής που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ft⋅lbf
Μεσαία θηράματα 1 ft⋅lbf
Πρασινοκέφαλη 2 ft⋅lbf
Χήνα 4 ft⋅lbf
Λαγός 1,5 ft⋅lbf
Αγριογούρουνο 90 ft⋅lbf
Η ελάχιστη διάτρηση καταβολής (σε 20% βαλλιστικό τζελ) που θεωρώ για κάθε θήραμα είναι οι ακόλουθες
Μικρά θηράματα 0,5 ίντσες
Μεσαία θηράματα 0,75 ίντσες
Πρασινοκέφαλη 1,5 ίντσες
Χήνα 2,25 ίντσες
Λαγός 1 ίντσα
Αγριογούρουνο 7 ίντσες
Οποιαδήποτε πρόταση για αλλαγή η αναφορά στο internet είναι δεκτή.
Μην ξεχνάμε ένα πολύ βασικό πράγμα ...
Τα παραπάνω δεν λαμβάνουν υπόψη την κατανομή και αναφέρονται σε 1 μόνο σκάγι !!!
Όταν βλέπετε λοιπόν αποστάσεις πχ 60m αυτό δεν σημαίνει ότι αν τουφεκίσετε το θήραμα στα 60 θα πέσει.
Σημαίνει ότι αν ένα ΜΟΝΑΔΙΚΟ σκάγι τύχει και χτυπήσει το θήραμα στα 60m αυτό το σκάγι θα έχει την ελάχιστη απαιτούμενη ενέργεια (που για κάποια θηράματα έχει οριστεί αυθαίρετα από εμένα) ή την ελάχιστη απαιτούμενη διάτρηση (που για κάποια θηράματα έχει οριστεί πάλι αυθαίρετα από εμένα).
Για τον @ΝίκοςΠ
Νίκο η διάτρηση που δίνω είναι σε 20% βαλλιστικό τζελ όχι σε χαρτί ή εξώφυλλα που είναι πιο χοντρά.
Το 20% βαλλιστικό τζελ προσομοιάζει ζωικό ιστό.
Όταν λοιπόν γράφω 1 ίντσα σε 20% βαλλιστικό τζελ σημαίνει ότι αν πάρεις ένα κομμάτι ψαχνό κρέας και το βάλεις στα μέτρα αυτά θα βρεις σκάγια που κατα μέσο όρο θα έχουν τρυπήσει το κρέας κατά 1 ίντσα = 25 χιλιοστά περίπου.
Κάποια δεν θα έχουν τρυπήσει καθόλου !!!!
Άλλα μπορεί να έχουν τρυπήσει 1,5 ίντσα.
Ο μέσος όρος είναι η 1 ίντσα.
Ελπίζω να σας έδωσα να καταλάβετε κάποια πράγματα περισσότερο και να μην σας μπέρδεψα.
Μην θεωρείτε ευαγγέλιο τα νούμερα, δείτε τα σαν ενδεικτικές τιμές και χρήσιμα για συγκρίσεις ....
Βασιλη μου......Απιστευτα μεγαλη η προσφορα σου για ολους ...και ειδικοτερα για μενα !!!
Κατανοητος και κατατοπιστικοτατος σε ολα....και απο εμενα ενα ΜΕΓΑΛΟ ΕΥΧΑΡΙΣΤΩ φιλε μου !!!

Μην μου βάζεις ξενα δεν ξέρω να διαβάσωΒεβαίως υψηλότερες ταχύτητες από τις 370 & 380 μ/δλ στην κάννη (Vo) της S4!
Δεδομένου οτι οι ταχύτητες είναι V 10 στο Ελληνικό διαφημιστικό φυλλάδιο , έχουμε:
V10 330 μ/δλ = Vo 402 μ/δλ & V10 340 μ/δλ = Vo 418 μ/δλ (!)
Δες το φυλλάδιο των 70s για σκάγια Νο 7 (!)
Θα βρω και το αλλο που λέει καταφέραμε να ξεπεράσουμε τα 390μ.δ με φυσίγγια Πυρκάλ.
Πολλα ''αχρηστα'' BAR + Διαφυγη αεριων...αν κρινω απο τον πατο του βυσματος και τα πεταλα που
ειναι καταμαυρα Στελιο !!!
- Status
- Not open for further replies.
Share:











